Zhichao Li

I am a Ph.D. candidate in the Department of Electrical and Computer Engineering at University of California, San Diego. I work at the Existential Robotics Laboratory and advised by Professor Nikolay Atanasov.

I received my M.S. degree from School of Electrical, Computer and Energy Engineering, Arizona State University in 2016. I received my B.Eng. degree from School of Astronatutics, Northwestern Polytechnical University in 2013.

Email  /  Google Scholar  /  Github

I am deeply passionate about the field of robotics, with a particular focus on the intersection of robotics, machine learning, control theory, and optimization. My research is centered around the development of safe, and robust control and planning algorithms for autonomous systems. I draw inspiration from the intricacies of the natural world, harnessing these insights to craft innovative algorithms and test them on real hardware platforms.

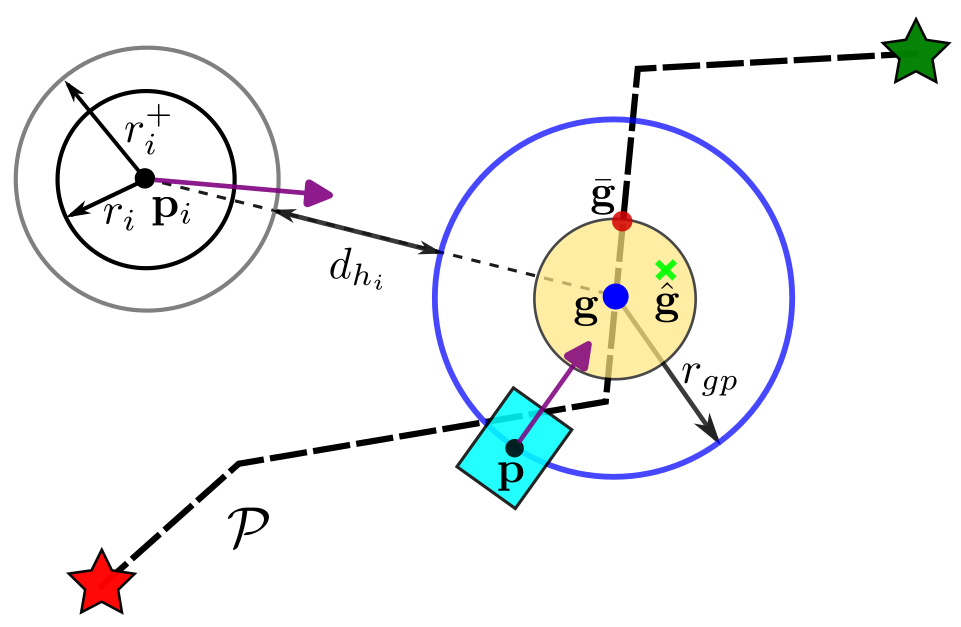
digram of active ref gvn control policy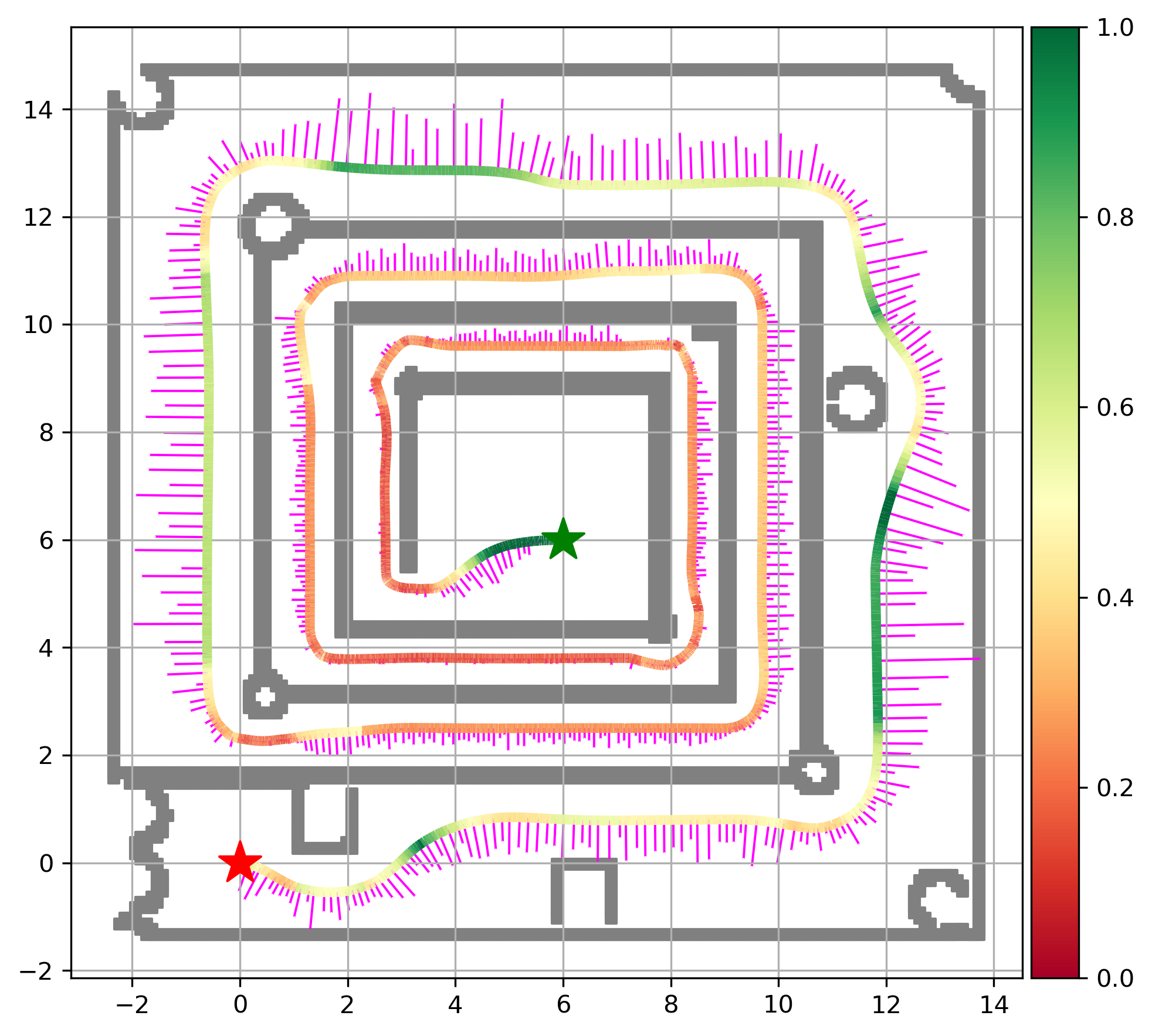

robot navigate adaptively through maze

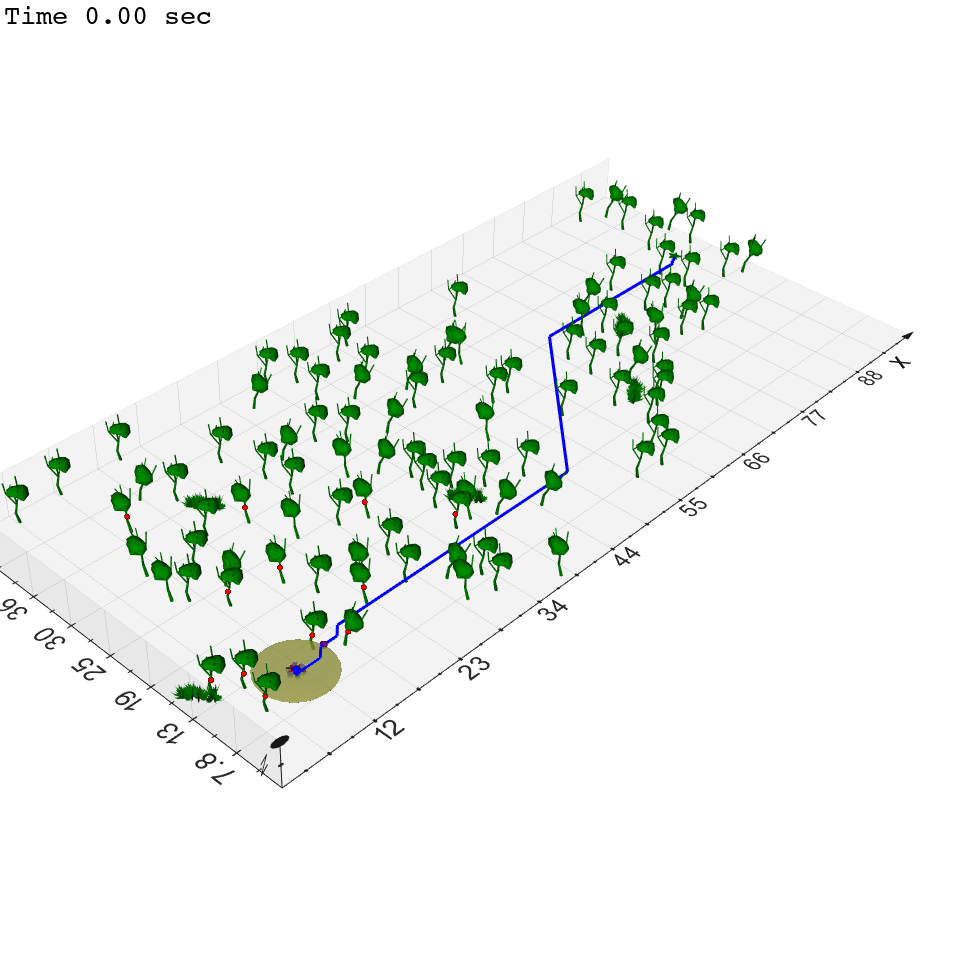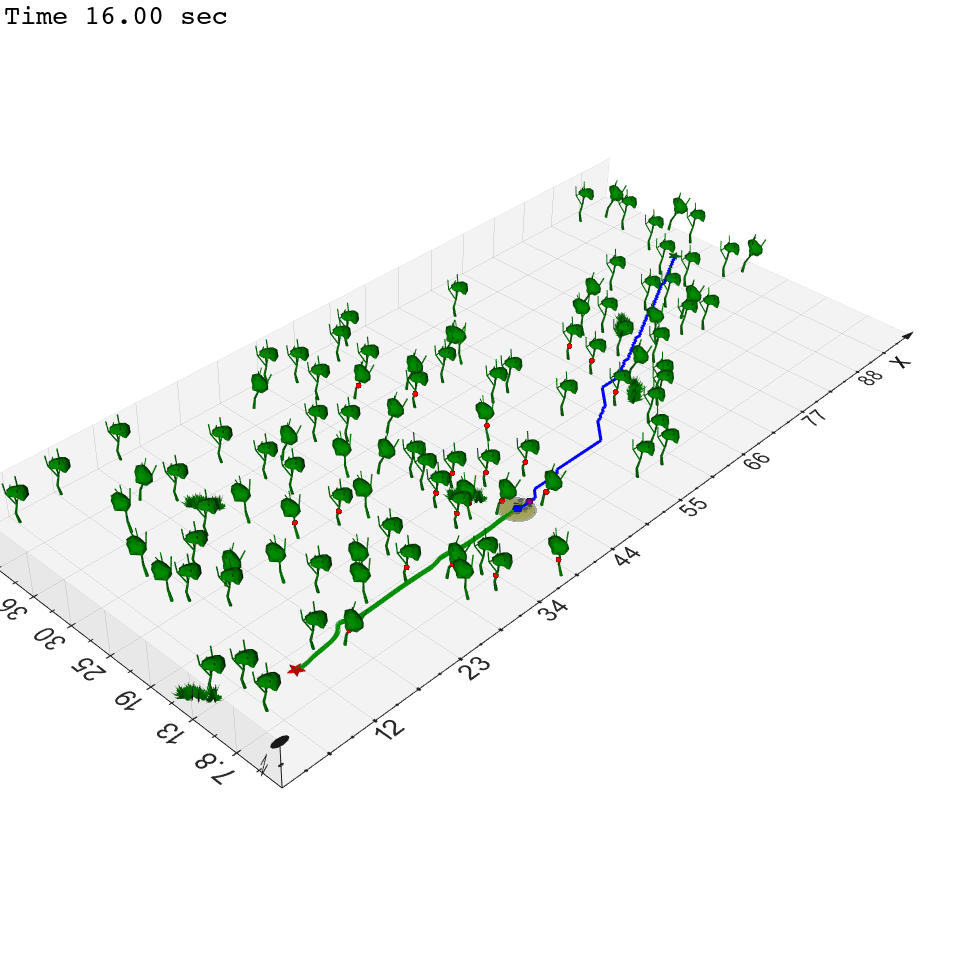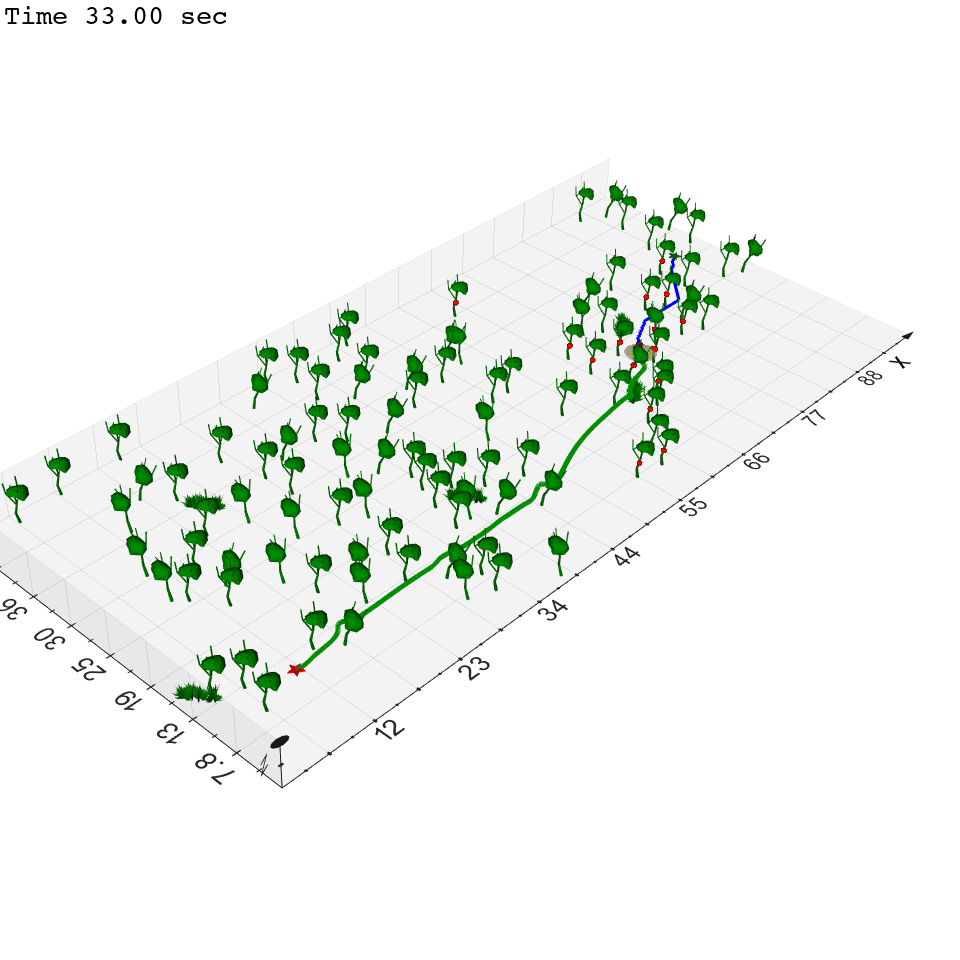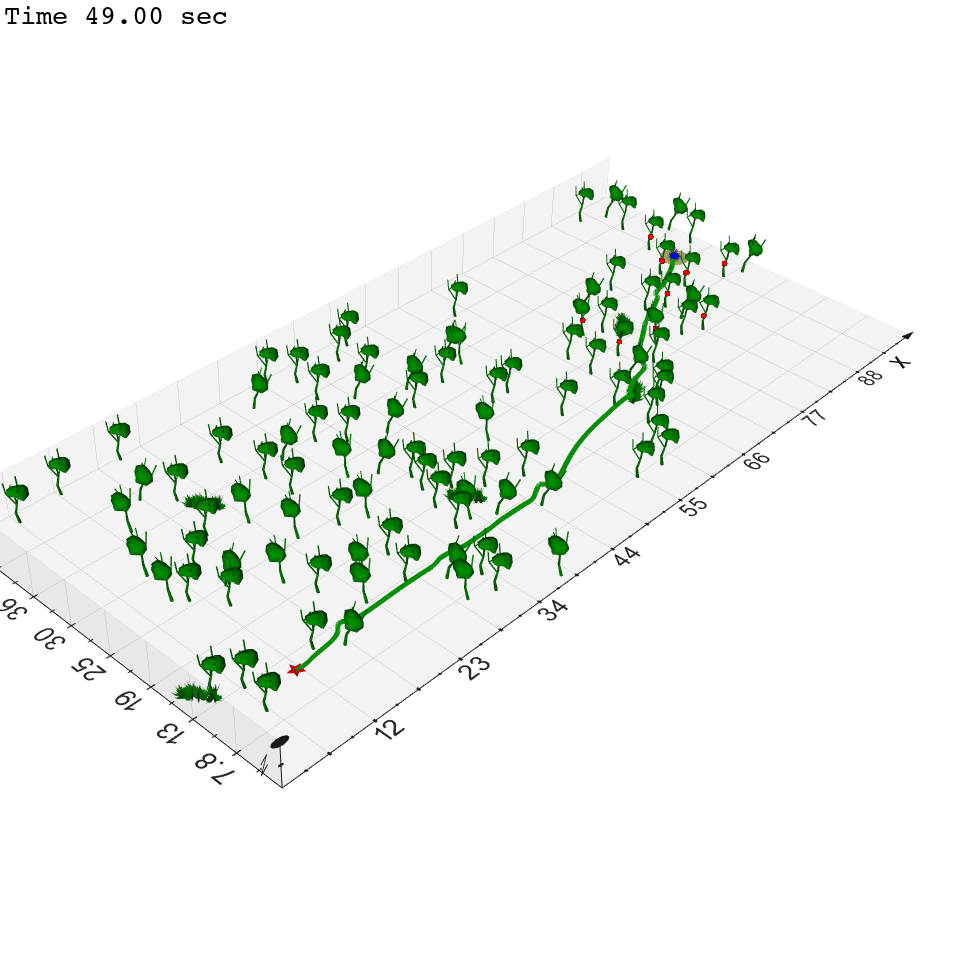
This paper considers the problem of autonomous robot navigation in unknown environments with moving obstacles. We propose a new method that systematically puts planning, motion prediction and safety metric design together to achieve environmental adaptive and safe navigation. This algorithm balances optimality in travel distance and safety with respect to passing clearance. Robot adapts progress speed adaptively according to the sensed environment, being fast in wide open areas and slow down in narrow passages and taking necessary maneuvers to avoid dangerous incoming obstacles. We validate our algorithm extensively both in simulation, large-scale indoor environments and challenging real-world environments with moving obstacles.

mobile robot with omnidirectional wheels

This paper considers output tracking with time-varying constraints, obtained from online sensor measurements. We develop a safe output tracking controller using reference governor techniques with governor-parameterized barrier function (G-PBF). Safe and stability analysis is discussed thoroughly. We demonstrate our adaptive output-tracking controller on a feedback-linearizable system navigating in an unknown environment, where obstacle distances are measured online.

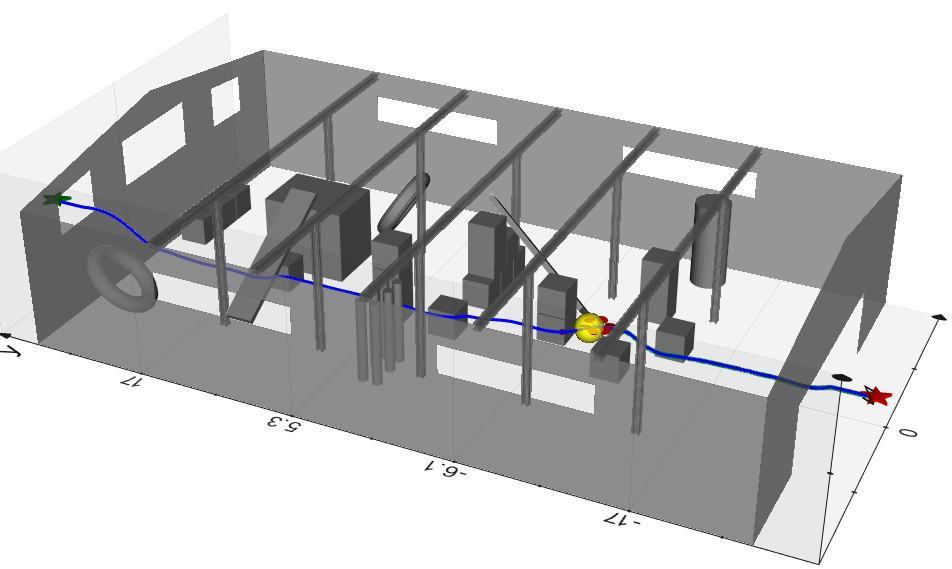
hexarotor flying through warehouse

This paper synthesize an energy-shaping passivity-based controller over an learned model and analyze its robustness to uncertainty. We extend our design using a reference governor to achieve 3D safe tracking control. Considering the system energy level, model uncertainty bounds, and distance to safety violation, the governor generates desired poses in SE(3) that move along the reference path adaptively to guarantee robustness and safety. Our Hamiltonian dynamics learning and tracking control techniques are demonstrated on simulated hexarotor and quadrotor robots navigating in cluttered 3D environments.

hexarotor flying through forest

This paper proposes techniques to learn the dynamics models of a mobile robot from trajectory data and synthesize a tracking controller with safety and stability guarantees. Instead of a hand-derived dynamics model, we use a dataset of state-control trajectories to train a translation-equivariant nonlinear Hamiltonian model represented as a neural ordinary differential equation (ODE) network. The learned Hamiltonian model is used to synthesize an energy-shaping passivity-based controller and derive conditions which guarantee safe regulation to a desired reference pose. Finally, we enable adaptive tracking of a desired path, subject to safety constraints obtained from obstacle distance measurements. Our safe adaptive controller is demonstrated on a simulated hexarotor robot navigating in unknown complex environments.

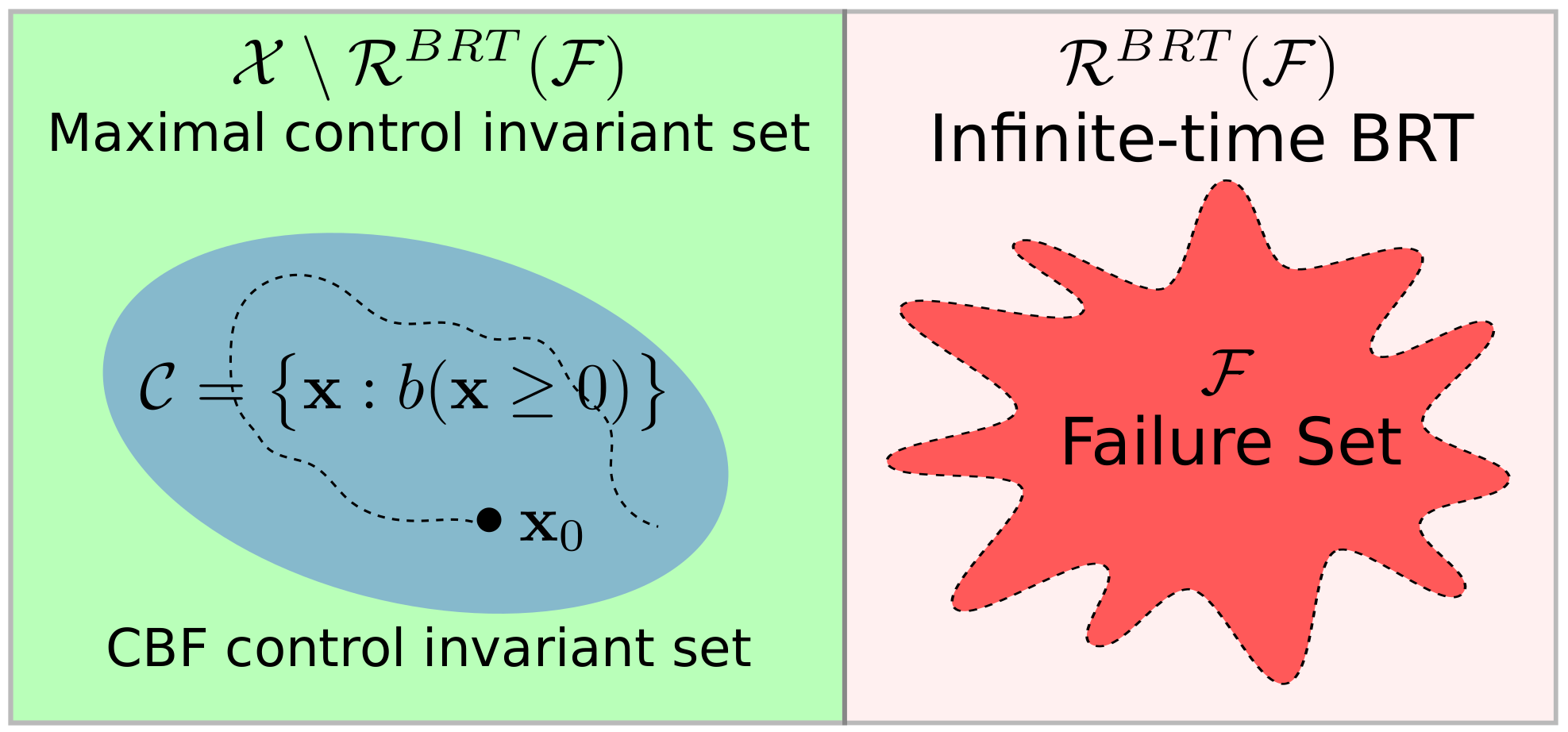
safe set characterization

This report aims to compare two methods for safe control: control barrier function and Hamilton-Jacobi reachability analysis. We will consider the difference with a focus on the following aspects: generality of system dynamics, difficulty of construction and computation cost. A standard Dubins car model will be evaluated numerically to make the comparison more concrete.

We consider a control-affine nonlinear robot system subject to bounded input noise and rely on feedback linearization to determine ellipsoid output bounds on the closed-loop robot trajectory under stabilizing control. A virtual governor system is developed to adaptively track a desired navigation path, while relying on the robot trajectory bounds to slow down if safety is endangered and speed up otherwise. The main contribution is the derivation of theoretical guarantees for safe nonlinear system path-following control and its application to autonomous robot navigation in unknown environments.

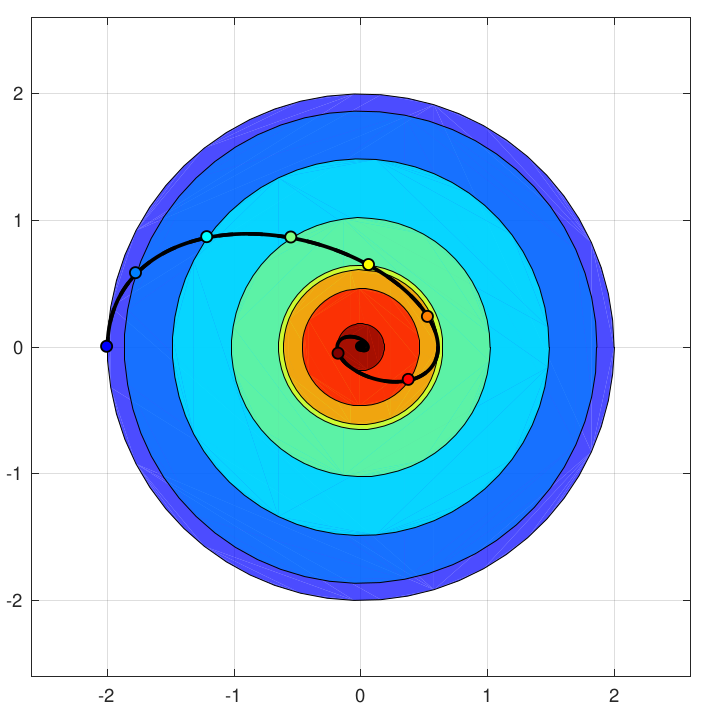
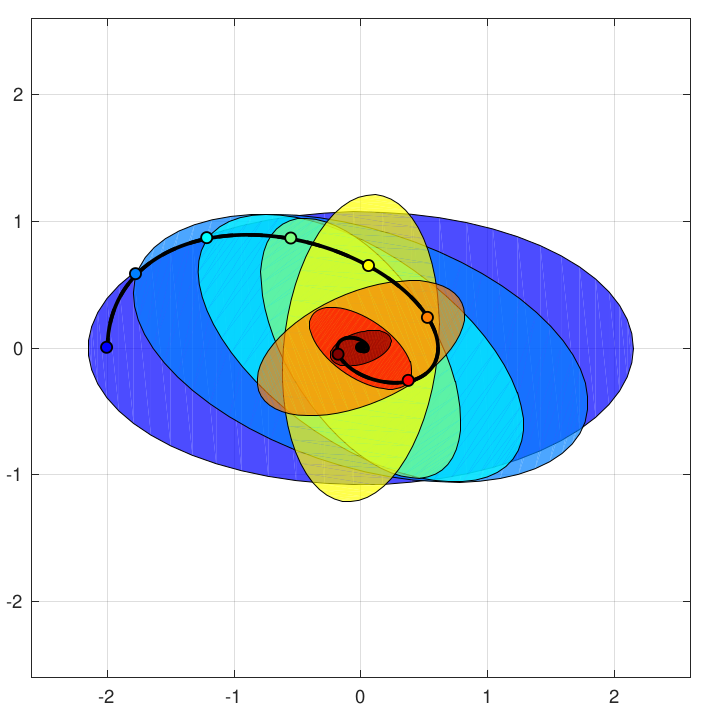
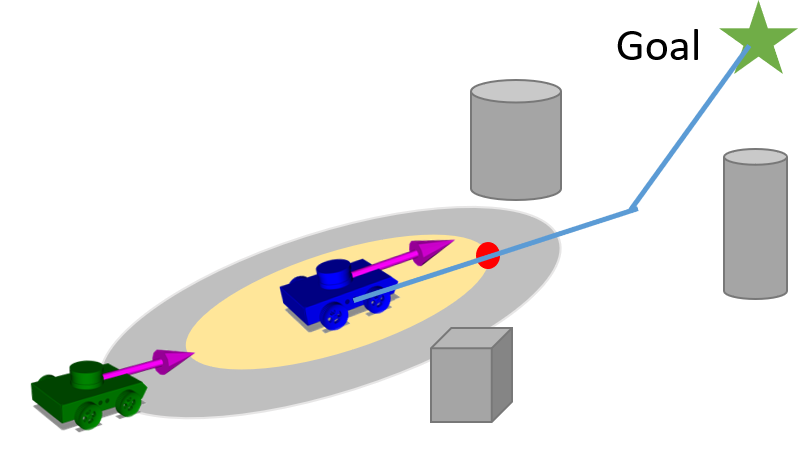
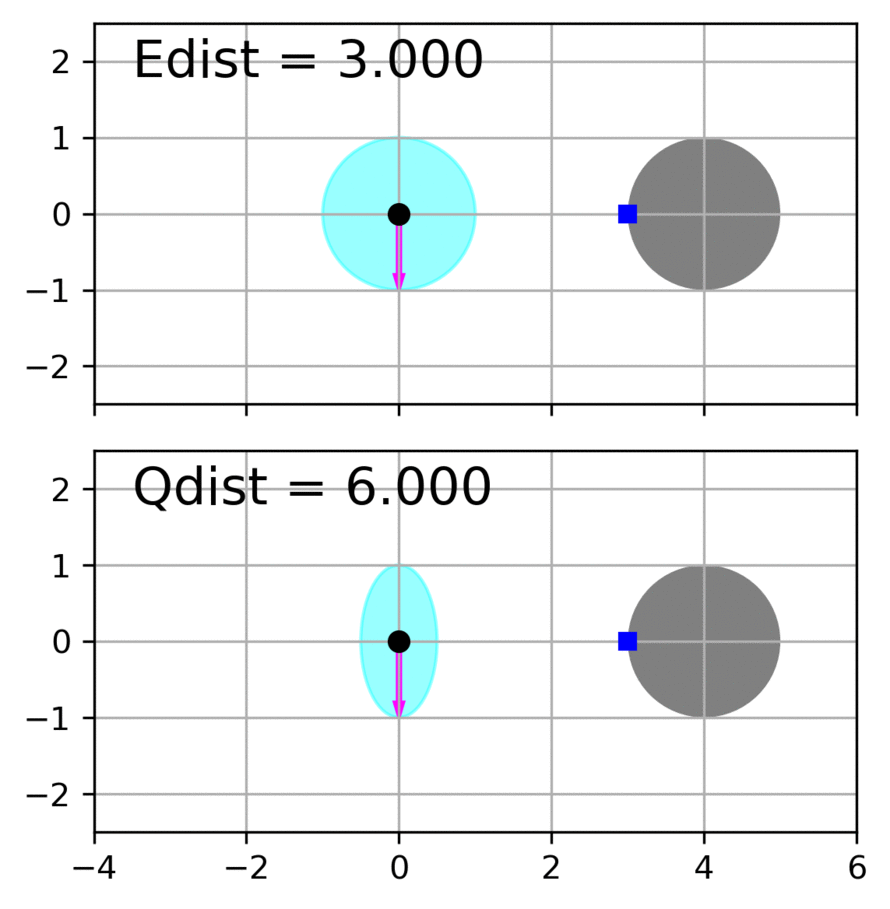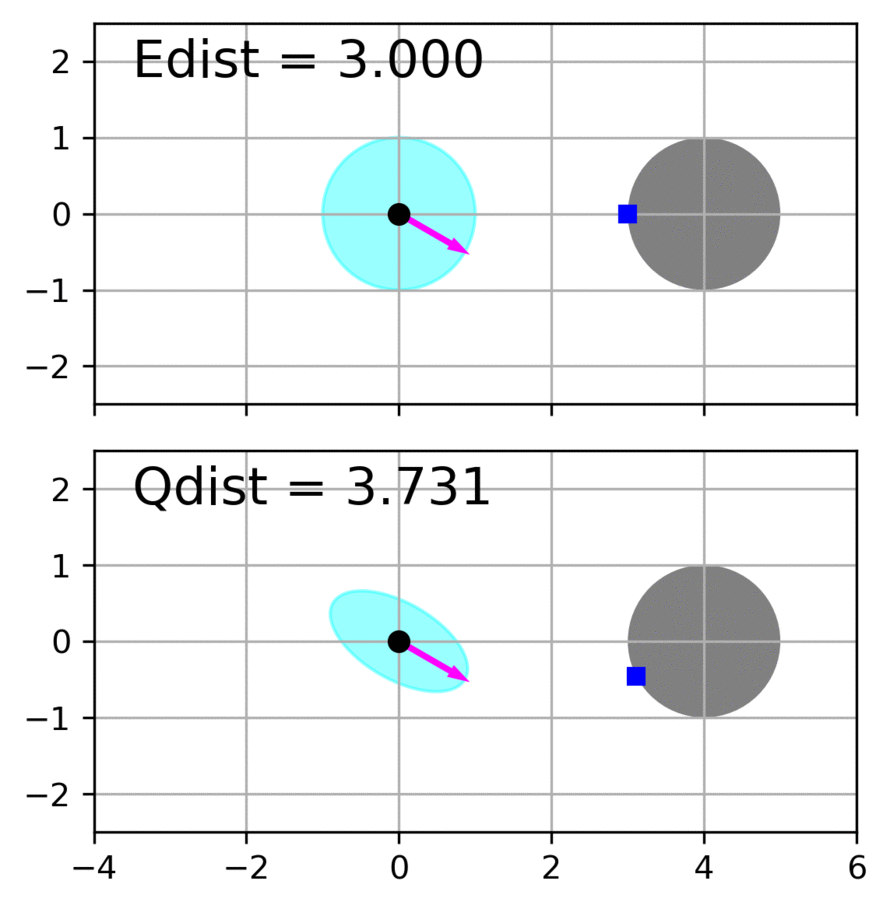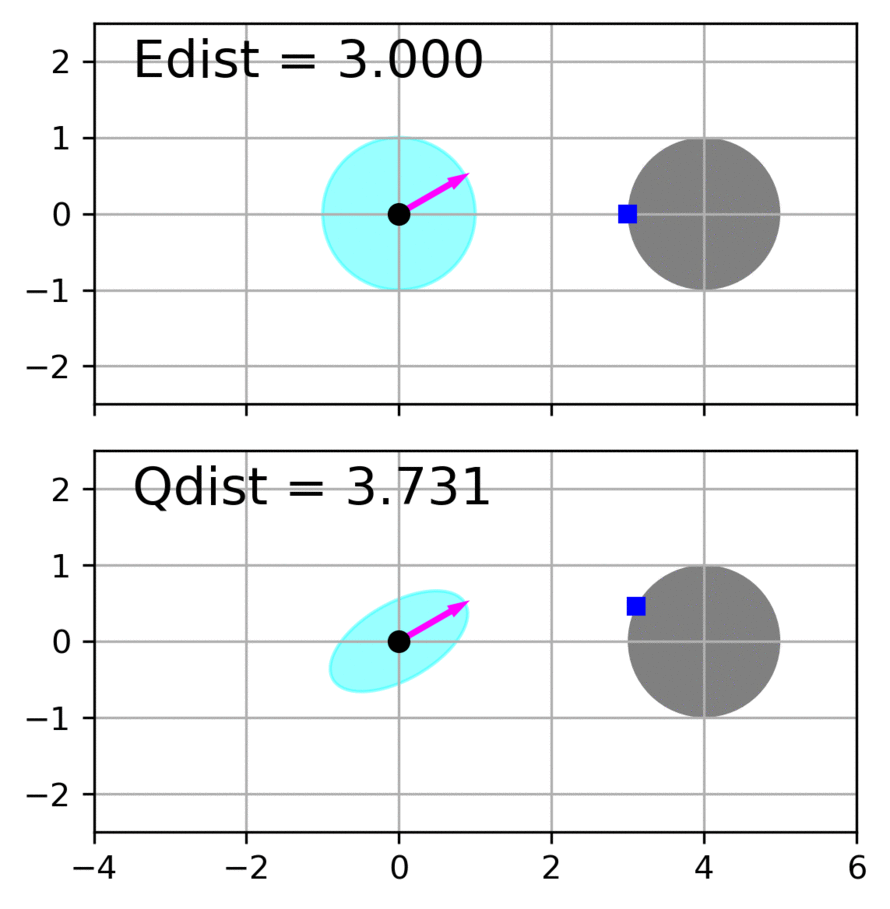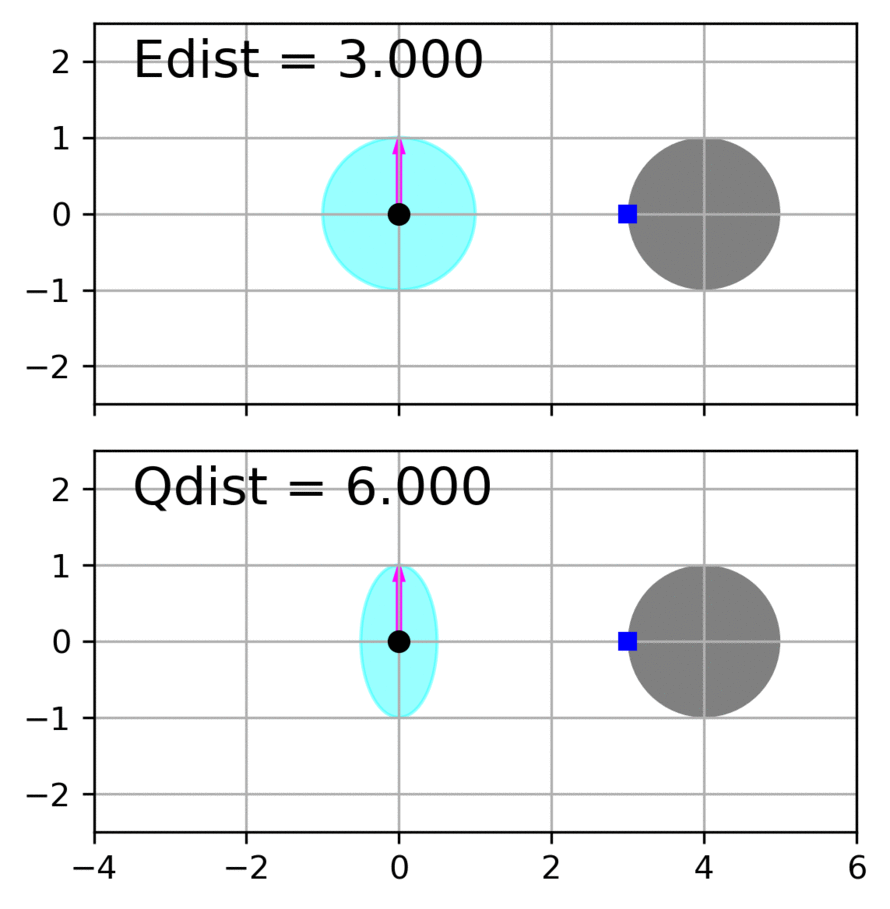
This paper considers the problem of fast and safe autonomous navigation in partially known environments. Our main contribution is a control policy design based on ellipsoidal trajectory bounds obtained from a quadratic state-dependent distance metric. The new metric leads to system behavior that is adapted to the local environment geometry, carefully considering medial obstacles while paying less attention to lateral ones. The resulting controller is able to navigate complex environments faster than common Euclidean-norm and Lyapunov-function-based designs, while retaining stability and collision avoidance guarantees.